Is Success Luck or Hardwork?

The world is full of hardworking, smart, ambitious, and lucky people. But how hardworking or lucky do you need to be successful? That is a hard question to answer (if I knew it I would already be handing out the formula on Twitter). There are many perspectives on this, for example, James Clear mentions that absolute success is luck, and relative success is hardwork.

Other perspectives (here, here, here, and here) also argue that most successful people overlook the role of luck in their success due to different psychological and cognitive biases.

Outliers by Malcolm Gladwell explains why the success of truly successful people is often a series of lucky events, rare opportunities and other external factors, which are out of their control. However, none of the methods actually try to quantify how much of success can be attributed to either variable. The closest I’ve seen to some quantitative treatment is a very cool video by Veritasium made a while ago (about 2 years before the time of writing this).

Most of the video made sense to me, except for the toy model of the astronaut selection process. The success of a participant was a weighted average of their skill/hardwork $h$ and luck $l$. Specifically, their final score is

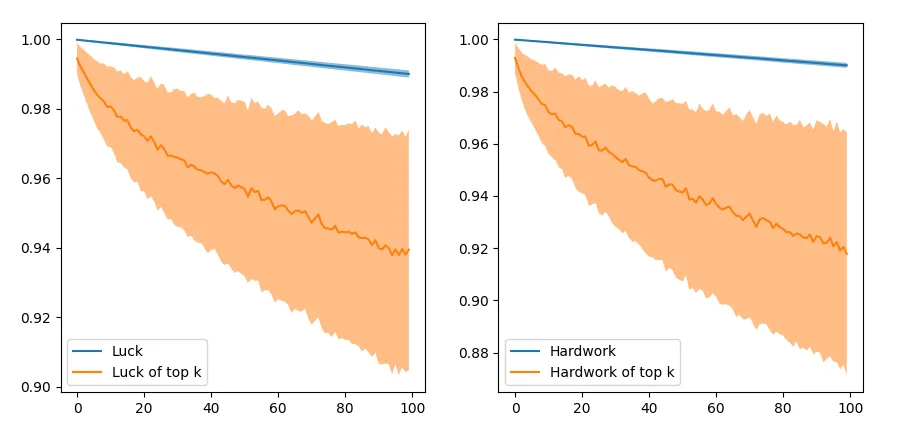
\[\text{score} = 0.95h + 0.05l\]

The video reports that the top 11 participants by this score had average luck of 94.7%, which actually is not very surprising. Top-ranked participants are likely to have high values of hard work and luck. What matters is the trend of the average luck versus hard work of the top-ranked participants.

Running a simulation reveals that the average luck is around 94.77% but the average hard work of those same 11 winners is around 99.72, showing that the average hard work matters much more for success. Not only that, I personally think that even for an exam scenario, this is an overly simplistic model, as it doesn’t account for extremely good or bad luck. I want to test out other models of luck and hardwork and draw conclusions based on the results, seeing if they match what we intuitively believe.

A (slightly) more rigorous treatment

To quantify how much of success is attributed to hard work and luck, we need to model the following:

• how do hard work and luck interact or influence each other?

• how is success defined as a function of hard work and luck?

These two questions can really spiral out of control if we are not careful. For example, modelling these interactions in everyday life will require some sequential model of luck, hard work, how they change over time, how interpersonal relationships affect these variables (for all people interacting in that relationship) and so on. For this case, we will consider a very simplistic scenario.

Consider a student preparing for an entrance exam like SAT (or JEE to relate to my Indian fellows reading this).

Consider a variable h which denotes the culmination of their skills, hard work, and preparation leading up to this day. I’m just gonna call it hard work for simplicity, but note that this variable is the “integral” of past luck combined with all the other variables (events like accidents or family events hindering the ability to study, or the school providing extra coaching classes all contribute to this variable).

The other variable under consideration is l, the luck of the student on the exam day. This luck can account for things like feeling sick on the day of the exam, or getting all questions from only the chapters the student studied, or getting some of your guessed answers correct (some personal anecdotes include my own experience in my entrance exam, where my exam center had a power outage in the last 20 minutes of the exam, or one of my friend, who guessed a series of multiple choice questions and got them all wrong!).

We will sample these values for 10000 students from some (reasonable) distributions and then define their exam score as a function of hard work and luck. Then we rank these scores, and repeat this experiment a 1000 times. Finally, we plot the average luck and hard work of these students as a function of their rank to see what matters more.

Model 1 - Hardwork and luck contribute independently

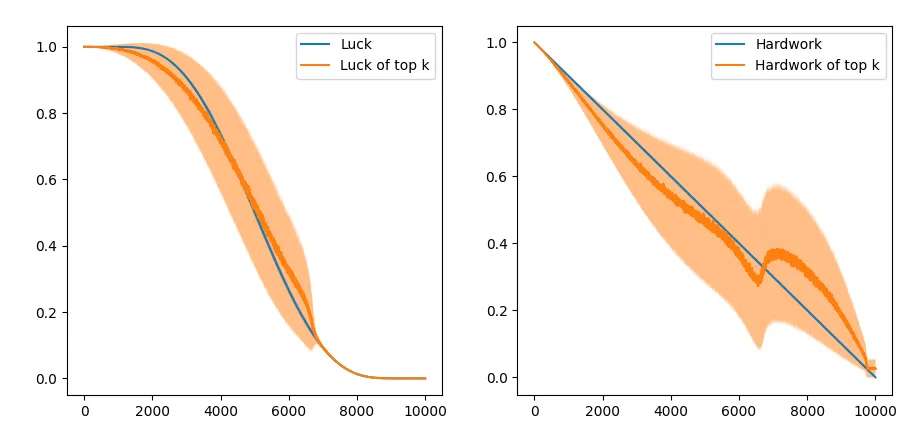
We sample the variables $h,l$ from the uniform distribution from $[0, 1]$, and define their score as the weighted arithmetic mean:

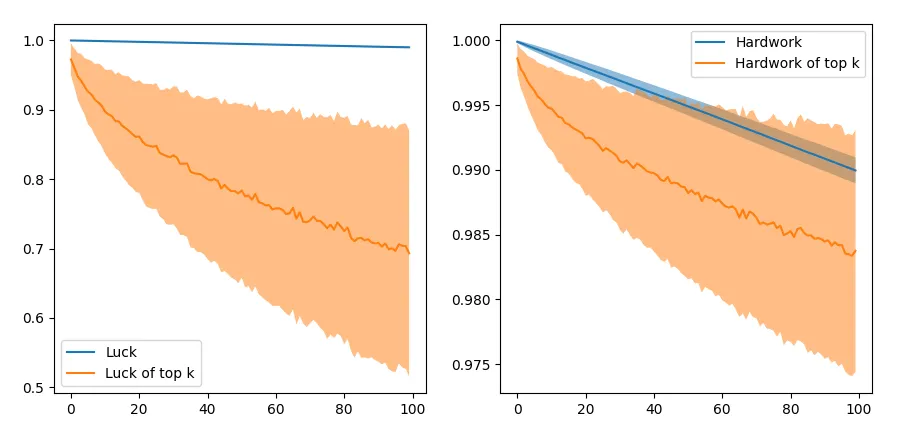
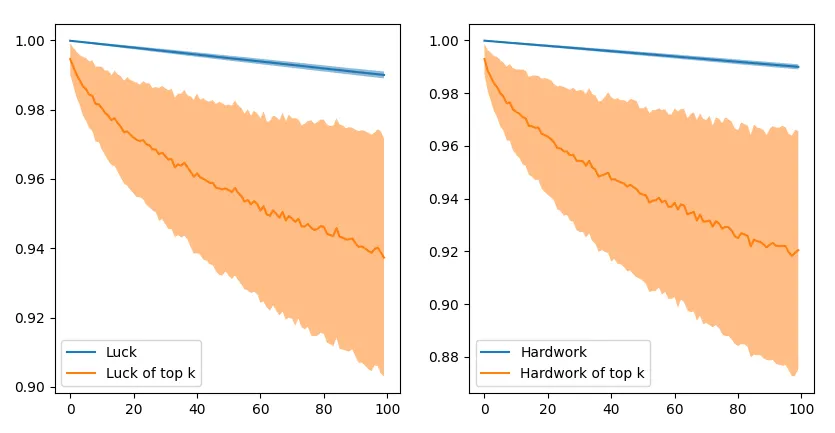
\[\text{score} = 0.95h + 0.05l\]

It is easy to see that this is not a good model, since a deficit of luck score by 0.95 can be made up with only a 0.05 amount of hard work. This is not very sensible because 0.95 can be the difference between someone extremely lucky or extremely unlucky. Plotting the average luck of the top 100 student reveals that on average these students have a much higher hard work than luck. The blue curve shows the hard work of the top 100 hardworking students (or lucky students) as a reference.

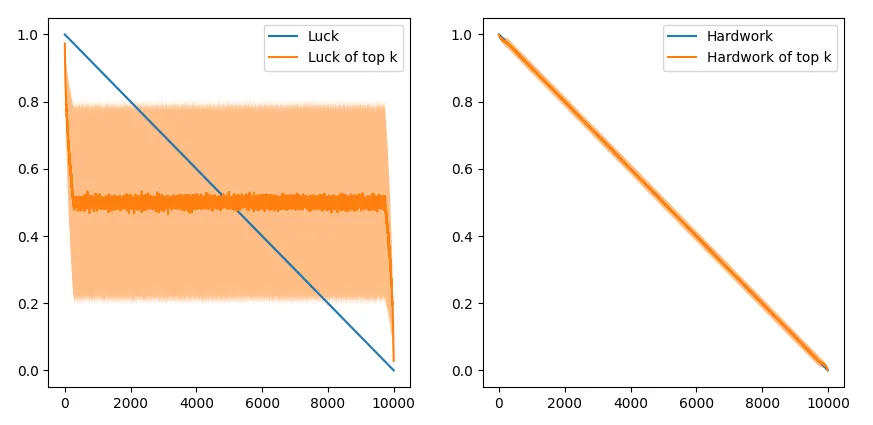
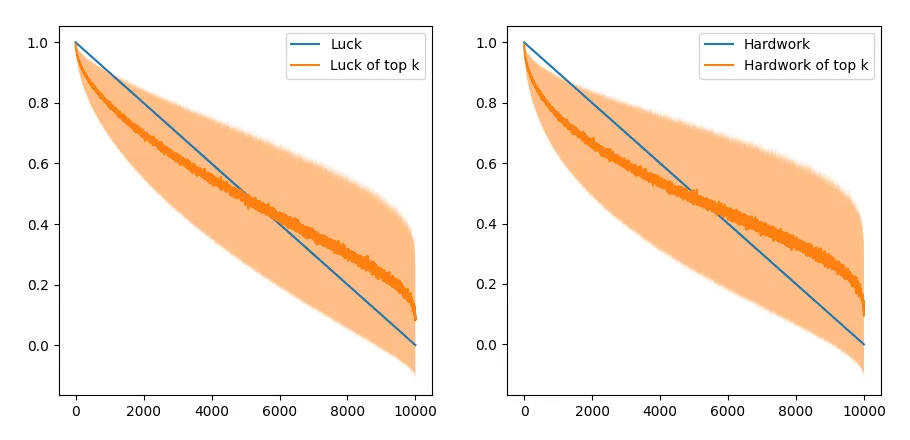
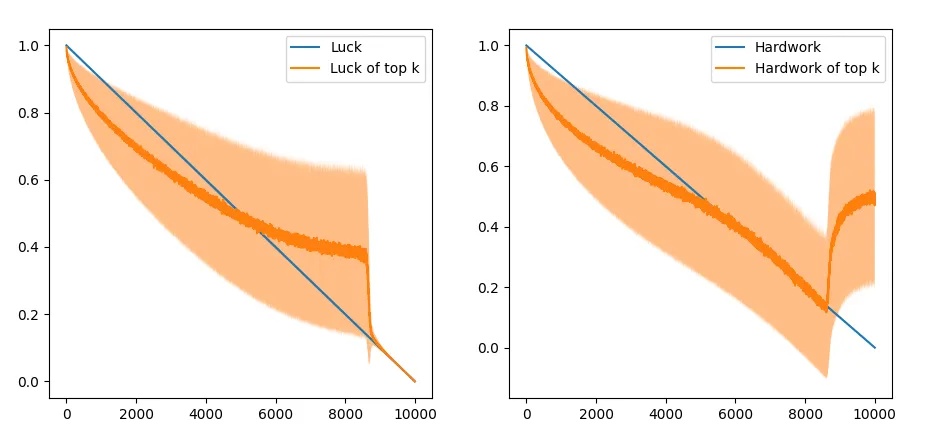
The top scores of all participants is also shown:

This is interesting - success seems to be more highly correlated with hard work than luck, although the top fraction of the students have disproportionately higher luck on average. The higher weight assigned to hard work essentially “blurs” the effect of luck over 1000 simulations.

Next, consider the weighted geometric mean (using the same weights):

\[\text{score} = h^{0.95} l^{0.05}\]

This seems to make more sense - a stroke of bad luck or low hard work can ramp your score down to 0 regardless of the other score. Let’s see how it works.

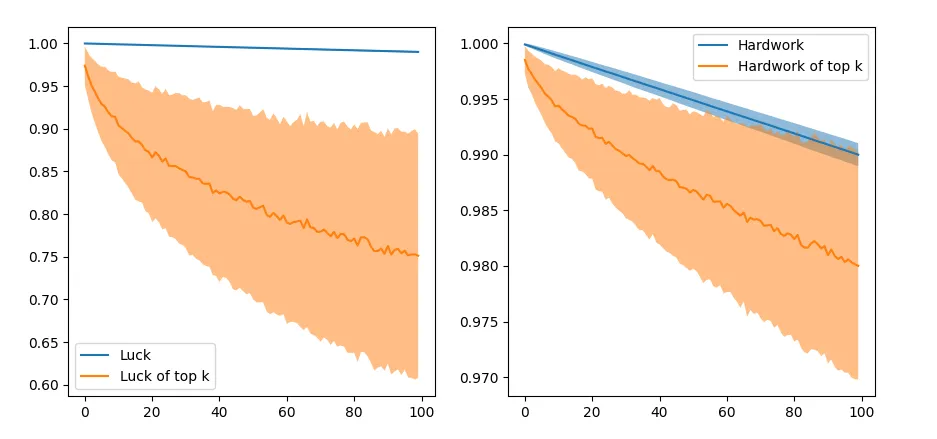
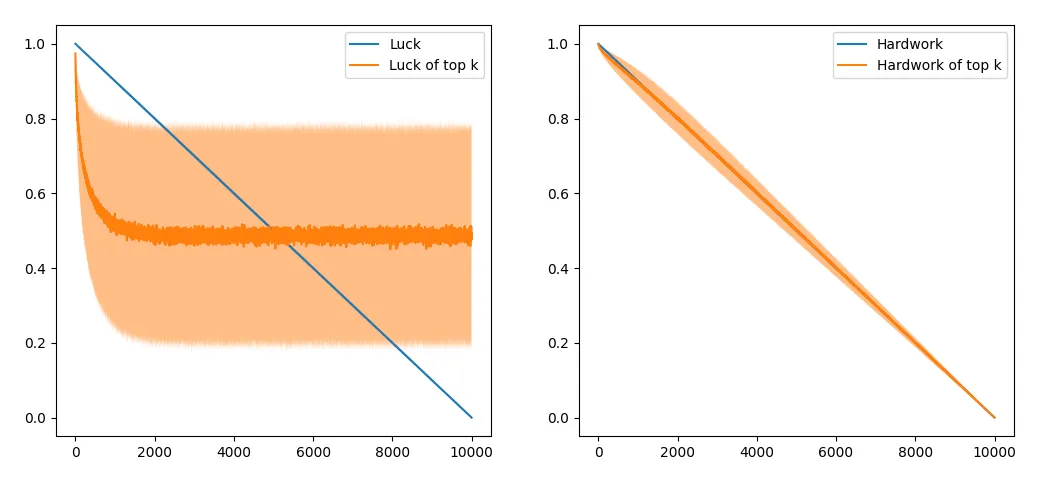
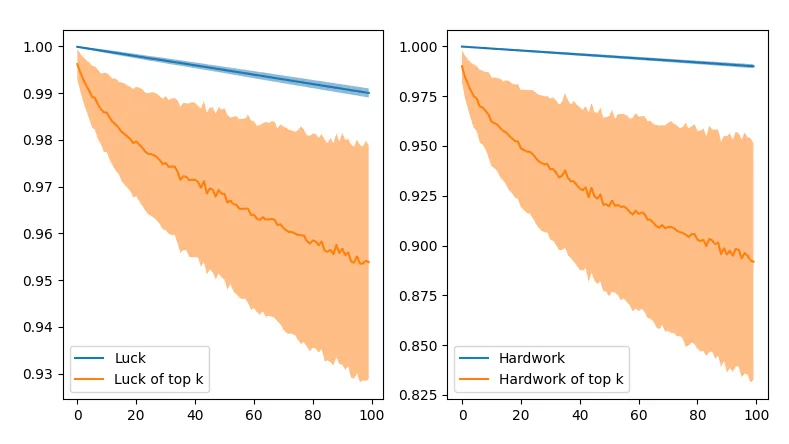
For the top 100 students, the trend doesn’t seem to change. Hardwork still seems to matter more than luck, even for all the students. This could again be due to the relative weight on hard work and luck.

Another important note is that hard work and luck contribute independently to the exam score, something that some people may find questionable. I had some discussions with some friends, who agree that hardwork increases the luck “surface area”, or that “hardworking people have good luck”. I wanted to independently test these two models too.

Model 2 - Hardwork increases the luck surface area

Another way of saying this is that luck amplifies the hard work of a student. An easy way to model this is this:

\[\text{score} = (1 + h)^l\]

I use $(1 + h)$ because using $h^l$ would make the score a decreasing function of $h$ 😅. The trends change a lot!

Now it seems like the average luck of the top 100 students more than the average hardwork. For all students, the trends look like this:

Now we try to increase the importance of hard work on the final score by the model:

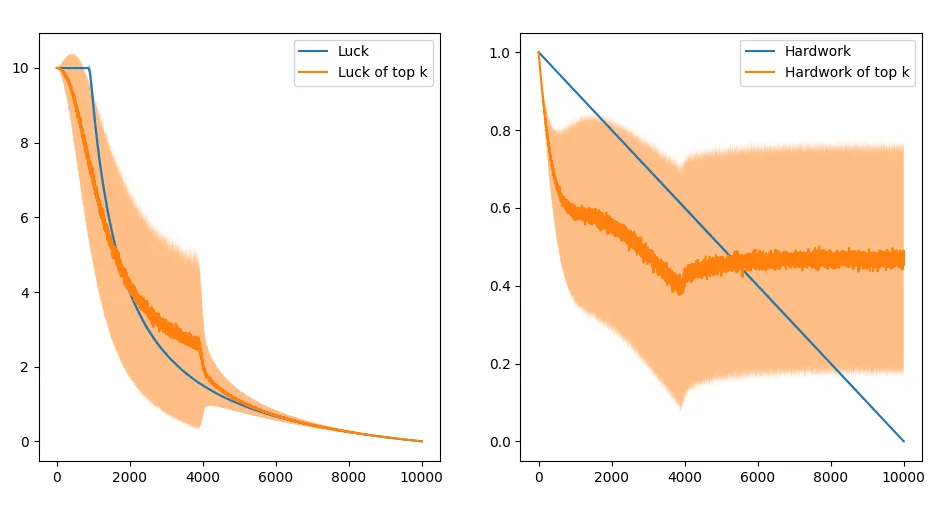
\[\text{score} = (1 + 10h)^l\]

We get a top 100 figure like this:

Note that compared to the previous top 100, the average luck increased and the average hard work reduced. So if you think that hard work amplifies luck, the more hard work contributes to (the formula for) success, the more actual success is to be attributed to luck.

---

Now we try adding a little bit of “bad luck”. Having a low luck score should sharply reduce the final score. We choose the following model for this:

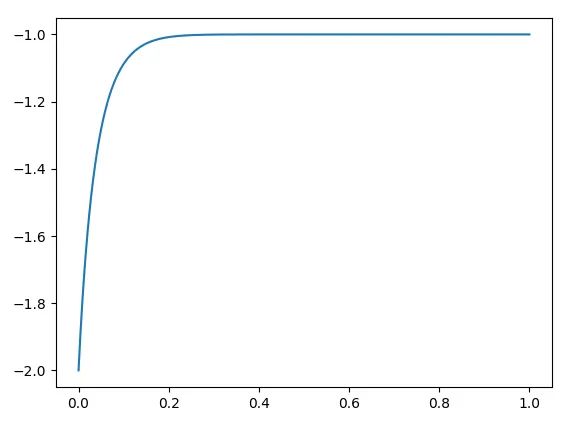
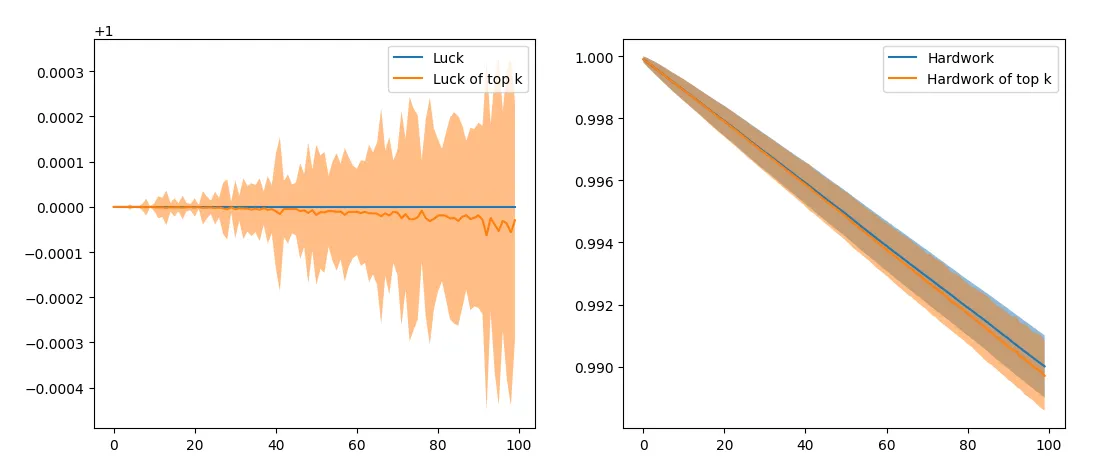
\[\text{score} = (1 + h)^l - 2^{(1 - l)^20}\]

We added the extra (negative) term, which looks like this (as a function of luck):

This looks reasonable - for most values of luck, its a constant, but for really low values of luck, this function becomes sharply negative. This “bad luck” is independent of hard work, which is also reasonable. Given this, the simulations look like the following:

Not very different from the previous graph - since top rankers do not have the bad luck term affecting them anyway. Now lets look at the overall population trends:

The most interesting part here is the last part of the curve - note the infinitesimally small variance of luck on the last $~20%$. These “bottom rankers” on average work as hard as the middle 40%, but their bad luck simply “overpowers” any hardwork they put in.

One of my friends suggested that luck follows a Pareto’s distribution. Let’s try that with the same model of score and hardwork! After making a few changes for numerical stability, we get this curve:

Again, this shows that the top scorers make disproportionately harder than the rest of the population, but most of the other people work equally hard on average, and it is primarily luck that determines their rank in this distribution.

Model 3 - Hardworking people have good luck

I will use the score function from model 2, but instead of sampling luck independently, I will sample luck from a distribution parameterized by the hard work.

Hardwork is sampled from the uniform distribution in $[0, 1]$. Therefore, a reasonable distribution for luck is to be sampled from the Beta distribution.

The reasoning is that the average of the samples from the Beta distribution will be the same as the hard work - therefore supporting the idea that “your luck is good if you worked hard and bad if you didn’t”. Furthermore, the beta distribution for hard work like a value of 0.5 peaks at both 0 and 1 (check this link for more details on this) - meaning that your luck can be either very good or very bad, if you’re someone with average skills or hardwork.

Here are the results for the top 100 students:

Note that for the top 100 students,the luck is very (and I mean very) close to 1. The hard work falls off a little faster than luck. Let’s look at the trends for the overall population:

Again, note the same “low rankers” having their rank primarily determined by luck, however, their luck is a function of hard work, so we observe a lower hard work than in the previous model.

Closing remarks

Looking at these graphs, and knowing that I’m far from covering all possible scenarios, I’ve come to the following conclusions:

• If you believe that luck amplifies hard work, then your success is mostly attributed to luck. This holds even more strongly if you increase the coefficient of hardwork in the formula for success. This also holds true even if luck is determined by hardwork (as some schools of thought also seem to suggest).

• Depending on how luck and hard work interact, success can be attributed more to hard work or luck. Anecdotally, people attribute a lot of absolute success to a series of fortunate events more than sheer work alone. In such a case, we should learn humility when we are successful, because we may simply be at the right place at the right time.

• In any scenario, success is a (generally) non-decreasing function of hard work (even when luck is marginalized out). Therefore, we must always work hard when we want to succeed. But when we actually succeed, we should be more careful about the role that luck played in this.

As a closing remark, I would like to mention the following phrase¹ from The Bhagavad Gita, the most revered Hindu text and a narrative by Lord Krishna:

You have the right to work, but never to the fruit of the work. You should never engage in action for the sake of reward, nor should you long for inaction.

Cheers!

1. Borrowed from Epicquotes. ↩︎